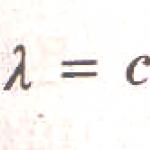• 07 октября 2016, 15:50
• Маркин Павел
• Печать

Упрощенный алгоритм вычисления приближенного значения размерности Минковского, для ценового ряда.

Краткая справка:

Размерность Минковского - это один из способов задания фрактальной размерности ограниченного множества в метрическом пространстве, определяется следующим образом:

• где N(ε) минимальное число множеств диаметра ε, которыми можно покрыть исходное множество.

Размерность Минковского имеет так же другое название - box-counting dimension , из-за альтернативного способа ее определения, который кстати дает подсказку к способу вычисления этой самой размерности. Рассмотрим двумерный случай, хотя аналогичное определение распространяется и на n-мерный случай. Возьмем некоторое ограниченное множество в метрическом пространстве, например черно-белую картинку, нарисуем на ней равномерную сетку с шагом ε, и закрасим те ячейки сетки, которые содержат хотя бы один элемент искомого множества.Далее начнем уменьшать размер ячеек, т.е. ε, тогда размерность Минковского будет вычисляться по вышеприведенной формуле, исследуя скорость изменения отношения логарифмов.

• комментировать
• Комментарии ( 23 )

Индикатор фрактального измерения FDI

• 16 апреля 2012, 18:17
• Chartist
• Печать

Подготовлено по материалам Эрика Лонга.

В данной работе сделана попытка «перевести» теорию фрактального анализа (работы Петерса, Мандельброта) для практического использования.
Хаос существует везде: во вспышках молний, погоде, землетрясениях и на финансовых рынках. Может показаться, что хаотические события случайны, но это не так. Хаос это динамическая система, которая кажется случайной, однако на самом деле представляет собой высшую форму порядка.
Социальные и природные системы, включая частные, правительственные и финансовые учреждения все подпадают под эту категорию. В каждой из систем, созданных людьми, существует множество взаимосвязанных вводных, которые влияют на систему самым непредсказуемым образом.
Когда мы обсуждаем теорию хаоса, применительно к торговле, мы ставим своей целью определить кажущееся случайным событие на рынке, которое, однако, имеет некоторую степень предсказуемости. Для этого нам необходим инструмент, который позволил бы представить хаотический порядок. Этим инструментом является фрактал. Фракталами называются объекты с автомодельными отдельными частями. На рынке, фракталом может быть назван объект или «временные последовательности», которые напоминают друг друга в разных временных диапазонах: 3-минутном, 30-минутном, 3-дневном. Объекты могут отличаться друг от друга на разных шкалах исследования, однако, если рассмотреть их отдельно они должны иметь общие черты для всех временных диапазонов.

Третьим свойством фракталов является то, что фрактальные объекты имеют размерность, отличную от Евклидовой (иначе говоря, топологическая размерность). Фрактальная размерность, является показателем сложности кривой. Анализируя чередование участков с различной фрактальной размерностью и тем, как на систему воздействуют внешние и внутренние факторы, можно научиться предсказывать поведение системы. И что самое главное, диагностировать и предсказывать нестабильные состояния.

В арсенале современной математики Мандельброт нашел удобную количественную меру неидеальности объектов – извилистости контура, морщинистости поверхности, трещиноватости и пористости объема. Ее предложили два математика – Феликс Хаусдорф (1868- 1942) и Абрам Самойлович Безикович (1891-1970). Ныне она заслуженно носит славные имена своих создателей – размерность Хаусдорфа – Безиковича. Что такое размерность и для чего она нам понадобится применительно к анализу финансовых рынков? До этого нам был известен только один вид размерности – топологическая (рис.3.11). Само слово размерность показывает, сколько измерений имеет объект. Для прямой линии она равна 1, т.е. мы имеем только одно измерение, а именно длину прямой. Для плоскости размерность будет 2, так как мы имеем двухмерное измерение, длина и ширина. Для пространства или объемных объектов, размерность равна 3: длина, ширина и высота.

Давайте рассмотрим пример с компьютерными играми. Если игра сделана в 3D графике, то она пространственна и объемна, если в 2D графике – графика изображается на плоскости (рис.3.10).

Самое необычное (правильнее было бы сказать – непривычное) в размерности Хаусдорфа – Безиковича было то, что она могла принимать не только целые, как топологическая размерность, но и дробные значения. Равная единице для прямой (бесконечной, полубесконечной или для конечного отрезка), размерность Хаусдорфа – Безиковича увеличивается по мере возрастания извилистости, тогда как топологическая размерность упорно игнорирует все изменения, происходящие с линией.

Размерность характеризует усложнение множества (например, прямой). Если это кривая, с топологической размерностью равной 1 (прямая линия), то кривую можно усложнить путем бесконечного числа изгибаний и ветвлений до такой степени, что ее фрактальная размерность приблизится к двум, т.е. заполнит почти всю плоскость (рис.3.12).

Увеличивая свое значение, размерность Хаусдорфа – Безиковича не меняет его скачком, как сделала бы «на ее месте» топологическая размерность, переход с 1 сразу к 2. Размерность Хаусдорфа – Безиковича – и это на первый взгляд может показаться непривычным и удивительным, принимает дробные значения: равная единице для прямой, она становится равной 1,15 для слегка извилистой линии, 1,2 – для более извилистой, 1,5 – для очень извилистой и т.д. (рис.3.13).

Именно для того чтобы особо подчеркнуть способность размерности Хаусдорфа – Безиковича принимать дробные, нецелые, значения, Мандельброт и придумал свой неологизм, назвав ее фрактальной размерностью. Итак, фрактальная размерность (не только Хаусдорфа – Безиковича, но и любая другая) – это размерность, способная принимать не обязательно целые, но и дробные значения.

Для линейных геометрических фракталов, размерность характеризует их самоподобность. Рассмотрим рис.3.17 (а), линия состоит из N=4 отрезков, каждый из которых имеет длину r =1/3. В итоге получаем соотношение:

D = logN/log(1/r)

Совсем дело обстоит иначе, когда мы говорим о мультифракталах (нелинейных объектах). Здесь размерность утрачивает свой смысл как определение подобия объекта и определяется посредством различных обобщений, куда менее естественных, чем уникальная размерность самоподобных линейных фракталов. В мультифракталах в роли показателя размерности выступает значение Н. Более подробно, мы рассмотрим это в главе «Определение цикла на валютном рынке».

Величина фрактальной размерности может служить индикатором, определяющим количество факторов, влияющих на систему. На валютном рынке размерностью можно охарактеризовать волатильность цены. Для каждой валютной пары характерно свое поведение. У пары GBP/USD поведение более импульсивное, нежели чем у EUR/USD. Самое интересное в том, что данные валюты двигаются одинаковой структурой к ценовым уровням, однако, размерность у них разная, что может сказаться на внутридневной торговле и на ускользающих от неопытного взгляда, изменениях в модели.

При фрактальной размерности менее 1.4, на систему влияет одна или несколько сил, двигающих систему в одном направлении. Если размерность около 1.5, то силы, действующие на систему, разнонаправлены, но более или менее компенсируют друг друга. Поведение системы в этом случае является стохастическим и хорошо описывается классическими статистическими методами. Если же фрактальная размерность значительно более 1.6, система становится неустойчивой и готова перейти в новое состояние. Отсюда можно сделать вывод, что чем более сложную структуру мы наблюдаем, тем все более возрастает вероятность мощного движения.

На рис.3.14 показана размерность применительно к математической модели, для того чтобы вы глубже прониклись в значение данного термина. Обратите внимание, что на всех трех рисунках изображен один цикл. На рис.3.14(а) размерность равна 1.2, на рис.3.14(б) размерность равна 1.5, а на рис.3. 14(в) 1.9. Видно, что с увеличением размерности восприятие объекта усложняется, возрастает амплитуда колебаний.

На финансовых рынках размерность находит свое отражение не только в качестве волатильности цены, но и в качестве детализации циклов (волн). Благодаря ей, мы сможем различать принадлежность волны к определенному масштабу времени.

На рис.3.15 изображена пара EUR/USD в дневном масштабе цен. Обратите внимание, четко видно сформировавшийся цикл и начало нового, большего цикла. Перейдя на часовой масштаб и увеличив один из циклов, мы сможем заметить более мелкие циклы, и часть крупного, расположенного в масштабе D1 (рис.3.16). Детализация циклов, т.е. их размерность, позволяет нам определить по начальным условиям, как может в дальнейшем развиваться ситуация. Мы можем сказать, что: фрактальная размерность отражает свойство масштабной инвариантности рассматриваемого множества.

Понятие инвариантности было введено Мандельбротом от слова «scalant» – масштабируемый, т.е. когда объект обладает свойством инвариантности, он имеет различные уровни (масштабы) отображения.

На рисунке кругом «А» выделен мини цикл (детализированная волна), кругом «Б» – волна большего цикла. Благодаря размерности волн, мы всегда сможем определить размер цикла.

Таким образом, можно сказать, что фракталы как модели применяются в том случае, когда реальный объект нельзя представить в виде классических моделей. А это значит, что мы имеем дело с нелинейными связями и недетерминированной (случайной) природой данных. Нелинейность в мировоззренческом смысле означает множество путей развития, наличие выбора из альтернативных путей и определенного темпа эволюции, а также необратимость эволюционных процессов. Нелинейность в математическом смысле означает, определенный вид математических уравнений (нелинейные дифференциальные уравнения), содержащих искомые величины в степенях, больше единицы или коэффициенты, зависящие от свойств среды.

Когда мы применяем классические модели (например, трендовые, регрессионные и т. д.), мы говорим, что будущее объекта однозначно детерминировано, т.е. полностью зависит от начальных условий и поддается четкому прогнозу. Вы самостоятельно можете выполнить одну из таких моделей в Excel. Пример классической модели можно представить в виде постоянно убывающей, либо возрастающей тенденции. И мы можем предсказать ее поведение, зная прошлое объекта (исходные данные для моделирования). А фракталы применяются в том случае, когда объект имеет несколько вариантов развития и состояние системы определяется положением, в котором она находится на данный момент. То есть мы пытаемся смоделировать хаотичное развитие, учитывая начальные условия объекта. Именно такой системой и является межбанковский валютный рынок.

Давайте теперь рассмотрим, как из прямой можно получить то, что мы называем фракталом, с присущими ему свойствами.

На рис.3.17(а) изображена кривая Коха. Возьмем отрезок линии, ее длина = 1, т.е. пока еще топологическая размерность. Теперь мы разделим ее на три части (каждая по 1/3 длины), и удалим среднюю треть. Но мы заменим среднюю треть двумя отрезками (каждый по 1/3 длины), которые можно представить, как две стороны равностороннего треугольника. Это стадия два (b) конструкции изображена на рис.3.17(а). В этой точке мы имеем 4 меньших доли, каждая по 1/3 длины, так что вся длина – 4(1/3) = 4/3. Затем мы повторяем этот процесс для каждой из 4 меньших долей линии. Это – стадия три (c) . Это даст нам 16 еще меньших долей линии, каждая по 1/9 длины. Так что вся длина теперь 16/9 или (4/3)2. В итоге получили дробную размерность. Но не только это отличает образовавшуюся структуру от прямой. Она стала самоподобной и ни в одной ее точке невозможно провести касательную (рис.3.17 (б)).

Понятия «фрактал» и «фрактальная геометрия» возникли в 70-80-х годах прошлого века. Они прочно вошли в обиход математиков и программистов. Слово «фрактал» происходит от латинского fractus, что в переводе означает дробный, состоящий из фрагментов. Оно было предложено американским математиком Бенуа Мандельбротом в 1975 году для обозначения нерегулярных («изломанных») самоподобных структур, которыми он занимался.

По определению, данному Мандельбротом, «фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому» . Фрактал - это бесконечно самоподобная геометрическая фигура, каждый фрагмент которой повторяется при уменьшении масштаба (см. рис. 6). Масштабная инвариантость, наблюдаемая во фракталах, может быть либо точной, либо приближённой.

Рисунок 6. Самоподобие фракталов на примере множества Мандельброта

С математической точки зрения фрактал - это, прежде всего, множество дробной размерности .

Рождение фрактальной геометрии принято связывать с выходом в 1977 году книги Мандельброта «Фрактальная геометрия природы», в которой автор собрал и систематизировал научные результаты ученых, работавших в период 1875-1925 гг. в той же области (Пуанкаре, Фату, Жюлиа, Кантор, Хаусдорф).

Фрактальная геометрия -- это революция в математике и математическом описании природы. Вот как об этом пишет сам первооткрыватель фрактальной геометрии Б.Мандельброт: «Почему геометрию часто называют холодной и сухой? Одна из причин заключается в ее неспособности описать форму облака, горы, дерева или берега моря. Облака -- это не сферы, горы -- это не конусы, линии берега -- это не окружности, и кора не является гладкой, и молния не распространяется по прямой. Природа демонстрирует нам не просто более высокую степень, а совсем другой уровень сложности» .

Мандельброт показал, что геометрия реального мира не евклидова, а фрактальная. «Правильные» евклидовы объекты являются математической абстракцией, природа же предпочитает негладкие, шероховатые, зазубренные формы. К евклидовой геометрии добавилась новая геометрия, отличие которой состоит в том, что она не оперирует гладкими объектами и привычными формами типа треугольника, квадрата, круга, шара и т.п. Фракталы с большой точностью описывают многие физические явления и природные образования. Снежинку, морского конька, ветви деревьев, разряд молнии и горные массивы можно нарисовать, используя фракталы. Поэтому многие современные ученые говорят о том, что природа имеет свойство фрактальности.

Фрактальная размерность

Главная особенность фрактальных объектов состоит в том, что для их описания недостаточно «стандартной» топологической размерности (для пространства, для поверхности - , для линии - , для точки), которая, как известно, всегда является целым числом. Под размерностью понимали минимальное число параметров, необходимых для описания положения точки в пространстве. Несостоятельность такого наивного восприятия стала очевидной после открытия взаимно однозначного соответствия между точками отрезка и квадрата и непрерывного отображения отрезка на квадрат (см. рис. 7). Первое из них было построено Кантором (1877 г.), второе -- Пеано (1890 г.).

Рисунок 7. Построение линии Пеано

Фракталам свойственна геометрическая «изрезанность». Поэтому используется специальное понятие фрактальной размерности, введенное Ф. Хаусдорфом и А.С. Безиковичем. Применительно к идеальным объектам классической евклидовой геометрии она давала те же численные значения, что и топологическая размерность, однако новая размерность обладала более тонкой чувствительностью ко всякого рода несовершенствам реальных объектов, позволяя различать и индивидуализировать то, что прежде было безлико и неразличимо. Этот тонкий инструмент позволяет сделать заключение, к какому обычному геометрическому объекту -- точке, линии или плоскости - ближе конкретное экзотическое фрактальное множество.

Мандельброт дал строгое математическое определение фрактала, как множества, хаусдорфова размерность которого, строго больше его топологической размерности. В то время как гладкая евклидова линия заполняет в точности одномерное пространство, фрактальная кривая вторгается в двумерное пространство, потому как ее размерность находится между 1 и 2. Фракталы - бесконечно-изломанные, «махровые» линии. Они напоминают гармошку, каждый кусочек которой, даже очень маленький, если попытаться его распрямить, оказывается бесконечно длинным.

Обсудим фрактальную размерность на примере регулярных фракталов (математическая абстракция). Рассмотрим сначала отрезок единичной длины, который разбит на равных кусков длиной, так что. По мере уменьшения значение растёт линейно, что и следовало ожидать для одномерной кривой. Аналогично, если мы разделим квадрат единичной площади на равных квадратиков со стороной, то получим - ожидаемый для двумерного объекта результат. Можно утверждать, что в общем случае, где - размерность объекта (см. рис. 8).

Рисунок 8. Покрытие объекта n-мерными кубиками

Следовательно, логарифмируя обе части этого равенства и перейдя к пределу при стремящемся к нулю, можно выразить размерность в виде:

Это равенство является определением хаусдорфовой или фрактальной размерности, которая обычно принимает дробные значения.

Приведем пример множества, состоящего из отдельных точек, но имеющих их столько, сколько и любой отрезок действительной оси. Возьмем отрезок длины 1. Разделив его на три равные части, исключим среднюю часть. С оставшимися двумя отрезками проделаем ту же процедуру и в результате получим 4 отрезка в 1/9 длины каждый и т.д. до бесконечности -- рис. 9.

Рисунок 9. Построение множества Кантора

Множество точек, возникшее после этой процедуры, и является множеством Кантора. Нетрудно заметить, что длина этого множества равна нулю. Действительно,

Найдем теперь его хаусдорфову или фрактальную размерность. Для этого выберем в качестве «эталона» отрезок длиной

Минимальное число таких отрезков, необходимых для покрытия множества, равно

Поэтому его фрактальная размерность

Также, размерность можно определить, исходя из зависимости изменения размеров той части пространства, которую занимает объект, от изменения его линейных размеров :

Для линии. Для плоскости. Для объема.

Проделаем такой эксперимент: возьмем равносторонний треугольник и будем последовательно заменять каждую линию, составляющую его, на четыре других, как это показано на рисунке 10.

Рисунок 10. Построение снежинки Кох

Повторяя эту операцию достаточно долго, мы получим некий объект, напоминающий своим внешним видом снежинку (называется - снежинка Кох), причем с каждым шагом длина кривой, ограничивающей площадь снежинки, увеличивается на одну треть. Ее размерность будет равна, так как при каждом увеличении снежинки в три раза длина кривой увеличивается в четыре. Если устремить число итераций к бесконечности, получится объект, конечная площадь которого ограничивается бесконечной кривой.

Мандельброт предложил следующее пробное определение фрактала:

Фракталом называется множество, размерность Хаусдорфа-Безиковича которого строго больше его топологической размерности

Это определение в свою очередь требует определений терминов множество, размерность Хаусдорфа-Безиковича и топологическая размерность которая всегда равна целому числу. Для наших целей мы предпочитаем весьма нестрогие определения этих терминов и наглядные иллюстрации (с использованием простых примеров), а не более строгое, но формальное изложение тех же понятий. Мандельброт сузил свое предварительное определение, предложив заменить его следующим

Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому.

Строгого и полного определения фракталов пока не существует . Дело в том, что первое определение при всей правильности и точности слишком ограничительно. Оно исключает многие фракталы, встречающиеся в физике. Второе определение содержит существенный отличительный признак, подчеркиваемый в нашей книге и наблюдаемый в эксперименте: фрактал выглядит одинаково, в каком бы масштабе его ни наблюдать. Взять хотя бы некоторые прекрасные кучевые облака. Они состоят из огромных «горбов», на которых возвышаются «горбы» поменьше, на тех - «горбы» еще меньше и т.д. вплоть до самого малого масштаба, который вы в состоянии разрешить. На самом деле, располагая только внешним видом облаков и не используя никакой дополнительной информации, размер облаков оценить невозможно.

Фракталы, о которых пойдет речь в этой книге, можно рассматривать как множества точек, вложенные в пространство. Например, множество точек, образующих линию в обычном евклидовом пространстве, имеет топологическую размерность и размерность Хаусдорфа - Безиковича Евклидова размерность пространства равна Так как для линии линия, согласно определению Мандельброта, не фрактальна, что подтверждает разумность определения. Аналогично множество точек, образующих поверхность в пространстве с имеет топологическую размерность Мы видим, что и обычная поверхность не фрактальна независимо от того, насколько она сложна. Наконец, шар, или полная сфера, имеет Эти примеры позволяют определить некоторые из рассматриваемых нами типов множеств.

Центральное место в определении размерности Хаусдорфа - Безиковича и, следовательно, фрактальной размерности занимает понятие расстояния между точками в пространстве. Как измерить «величину»

множества У точек в пространстве? Простой способ измерить длину кривых, площадь поверхностей или объем тела состоит в том, чтобы разделить пространство на небольшие кубы с ребром 8, как показано на рис. 2.5. Вместо кубов можно было бы взять небольшие сферы диаметром 8. Если поместить центр малой сферы в какой-нибудь точке множества, то все точки, находящиеся от центра на расстоянии окажутся покрытыми этой сферой. Подсчитывая число сфер, необходимых для покрытия интересующего нас множества точек, мы получаем меру величины множества. Кривую можно измерить, определяя число прямолинейных отрезков длины 8, необходимых для того, чтобы покрыть ее. Разумеется, для обычной кривой Длина кривой определяется предельным переходом

В пределе при мера становится асимптотически равной длине кривой и не зависит от 8.

Множеству точек можно поставить в соответствие и площадь. Например, площадь кривой можно определить, указывая число кругов или квадратов, необходимых для ее покрытия. Если -число этих квадратов, а -площадь каждого из них, то площадь кривой равна

Аналогично объем V кривой можно определить как величину

Рис. 2.5. Измерение «величины» кривой.

Разумеется, что для обычных кривых обращаются в нуль при , и единственной представляющий интерес мерой является длина кривой.

Как нетрудно видеть, для обычной поверхности число квадратов, необходимых для ее покрытия, определяется в пределе при выражением где площадь поверхности.

Поверхности можно поставить в соответствие объем, образуя сумму объемов кубов, необходимых для покрытия поверхности:

При этот объем, как и следует ожидать, обращается в нуль.

Можно ли поверхности поставить в соответствие какую-нибудь длину? Формально мы можем принять за такую длину величину

которая расходится при Этот результат имеет смысл, так как поверхность невозможно покрыть конечным числом прямолинейных отрезков. Мы заключаем, что единственной содержательной мерой множества точек, образующих поверхность в трехмерном пространстве, является площадь.

Нетрудно видеть, что множества точек, образующих кривые, могут

Рис. 2.6. Измерение «величины» поверхности.

быть закрученными так сильно, что длина их окажется бесконечной, и, действительно, существуют кривые (кривые Пеано), заполняющие плоскость. Существуют также поверхности, изогнутые столь причудливым образом, что они заполняют пространство. Для того чтобы мы могли рассматривать и такие необычные множества точек, полезно обобщить введенные нами меры величины множества.

До сих пор, определяя меру величины множества точек У в пространстве, мы выбирали некоторую пробную функцию отрезок прямой, квадрат, круг, шар или куб - и покрывали множество, образуя меру Для прямолинейных отрезков, квадратов и кубов геометрический коэффициент для кругов и для сфер Мы заключаем, что в общем случае при мера равна нулю или бесконечности в зависимости от выбора -размерности меры. Размерность Хаусдорфа-Безиковича множества есть критическая размерность, при которой мера изменяет свое значение с нуля на бесконечность:

Мы называем -мерой множества. Значение при часто конечно, но может быть равно нулю или бесконечности; существенно, при каком именно значении величина изменяется скачком. Заметим, что в приведенном выше определении размерность Хаусдорфа-Безиковича фигурирует как локальное свойство в том смысле, что эта размерность характеризует свойства множеств точек в пределе при исчезающе малом диаметре, или размере, 8 пробной функции, используемой для покрытия множества. Следовательно, фрактальная размерность может также быть локальной характеристикой множества. В действительности здесь существует несколько тонких пунктов, заслуживающих рассмотрения. В частности, определение размерности Хаусдорфа-Безиковича позволяет покрывать множество «шарамтк не обязательно одного и того же размера при условии, что диаметры воех шаров меньше 8. В этом случае -мера есть нижняя грань, т. е., грубо говоря, минимальное значение, получаемое при всех возможных покрытиях. Примеры см. в разд. 5.2. Строгое математическое изложение вопроса интересующиеся найдут в книге Фальконера .

Введение во фракталы

Основы теории фракталов

Методы определения фрактальных характеристик объектов

Чтобы понять природу, человек строит объекты различной геометрии. В природе объекты встречаются самых разных размеров - от атомных масштабов до Вселенной. Геометрия траекторий частиц, линий тока в гидродинамике, волн, обводов корабельных корпусов и береговых линий, ландшафтов, гор, ост­ровов, рек, ледников и отложений, зерен в скалистых породах, металлах и ком­позитных материалах, растений, насекомых и живых клеток, а также геометри­ческая структура кристаллов, молекул химических веществ и, в частности, про­теинов - словом, геометрия природы занимает центральное место в различных областях естествознания, и поэтому люди склонны считать геометрические ас­пекты чем-то само собой разумеющимся. Представители каждой области стре­мились развить свои приспособленные к ее потребностям понятия (например, такие, как морфология, четырехмерное пространство, текстура), интуитивно используемые учеными, работающими именно в этой области. По традиции, основой интуитивного понимания геометрии природы служили евклидовы прямые, окружности, сферы, тетраэдры и т.п.

Математики разработали и математические понятия, выходившие за рамки традиционной геометрии, однако, в прошлом эти понятия не привлекли к себе должного внимания со стороны представителей естественных наук из-за весьма абстрактного и «педантичного» изложения и из-за предостережений относи­тельно «опасности», связанной с использованием такого рода нетрадиционных геометрических представлений.

Своими яркими и фундаментальными работами Бенуа Мандельброт про­будил всеобщий интерес к фрактальной геометрии - понятию, введенному са­мим Мандельбротом. В частности, он поведал миру об объектах, названных им фракталами, избрав для этого весьма необычную форму изложения. Книга Бе­нуа Мандельброта «Фрактальная геометрия природы» - общепризнанный стандартный справочник по фракталам, содержащий как элементарные поня­тия, так и необычайно широкий круг новых и отнюдь не элементарных идей, находящихся сейчас в центре внимания тех, кто занимается геометрией фракта­лов. Синтетические фрактальные пейзажи выглядят настолько правдоподобно, что большинство людей принимают их за естественные. Появление в последние годы компьютеров и компьютерной графики привело к исследованию нетради­ционных геометрических объектов во многих областях естественных наук.

Мандельброт написал огромное количество научных работ, посвященных геометрии явлений, наблюдаемых во многих областях человеческой деятельно­сти. Он исследовал фрактальную геометрию изменений цен и распределений заработной платы, статистики ошибок при вызовах на телефонных станциях, частот слов в печатных текстах, различных математических объектов и многого другого. Мандельброт написал три книги о фрактальной геометрии, сделавшие более доступными его специальные работы и вдохновившие многих на приме­нение фрактальной геометрии в области собственных исследований.

Понятие «фракталы» захватило воображение ученых, работающих во мно­гих областях науки, и работы, в которых фракталы обсуждаются с самых раз­ных позиций, появляются теперь почти ежедневно. Книги Мандельброта заме­чательны в нескольких отношениях. И прежде всего - они междисциплинарны: автор рассматривает геометрию деревьев, русел рек, легких, а также изменения уровней водной поверхности, турбулентность, экономику, частоты появления слов в различных текстах и многое-многое другое. Все эти, казалось бы, разно­родные вопросы Мандельброт связывает со своими геометрическими представ­лениями. В своих книгах он умышленно избегает введений и заключений, тем самым подчеркивая свое глубокое убеждение в том, что по мере расширения работ в области фрактальной геометрии, его идеи позволят все более глубоко постигать самую суть геометрии природы. Он предлагает лишь пробное опре­деление понятия «фрактал» и тут же поспешно заявляет, что предложенное им определение отнюдь не является окончательным! Более того, впоследствии он отказывается от своего определения. В своих книгах Мандельброт пытается убедить читателя в том, что фрактальная геометрия важна для описания приро­ды, но ускользает от читателя, когда тот пытается проследить за деталями ар­гументации автора. Математические доказательства перемешиваются на стра­ницах книг Мандельброта с анекдотами и историческими сведениями. Совер­шенно разные вопросы перемешаны в его книгах так, что разделить их практи­чески невозможно. Но, вооружившись терпением, любознательный читатель найдет в книгах Мандельброта необычайно широкий спектр замечательных идей, глубоких замечаний и сможет почерпнуть в них подлинное вдохновение -эти книги поистине замечательны!

Наиболее сильное впечатление производят цветные иллюстрации. На них изображены фрактальная «планета», восходящая над горизонтом своей луны, горы, долины и острова, которых никогда не было. Эти иллюстрации, выпол­ненные Р.Ф. Фоссом, получены с помощью алгоритмов, обеспечивающих фрак­тальную природу пейзажей. Все пейзажи выглядят очень естественно, по-видимому, фракталы каким-то образом схватывают суть топографии земной поверхности.

Понятия «фрактал» и «фрактальная геометрия», появившиеся в конце 70-х, с середины 80-х прочно вошли в обиход математиков и программистов. Слово фрактал образовано от латинского fractus и в переводе означает «состоящий из фрагментов». Оно было предложено Бенуа Мандельбротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимал­ся. В его работах использованы научные результаты трудов ученых, работав­ших в 1875-1925 годах в той же области (Пуанкаре, Фату, Жюлиа, Кантор, Хаусдорф и другие). Но только в наше время удалось объединить их работы в единую систему.

Внимание, которое привлекают фракталы, видимо, имеет несколько при­чин. Во-первых, фракталы очень просты при моделировании многих явлений и процессов, которые трудно отличить от естественных. Во-вторых, при фрак­тальном анализе процессы сложной формы представляются в достаточно про­стой и наглядной форме, что позволяет получить больше информации о про­цессе.

В настоящее время, наибольшее применение фракталы нашли в машинной графике и компьютерных системах сжатия информации. Они приходят на по­мощь, например, когда требуется с помощью нескольких коэффициентов задать линии и поверхности очень сложной формы. С точки зрения машинной графи­ки, фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря. Фактически найден способ легкого представления сложных неевклидовых объектов, образы которых весьма похожи на природ­ные.

Фракталом, по определению Мандельброта, называется объект, размер­ность которого не равна его топологической размерности и может принимать нецелочисленные значения. Такая размерность называется размерностью Хаусдорфа-Безиковича или фрактальной размерностью. Многочисленные исследо­вания показывают, что фрактальная геометрия является обобщением евклидо­вой, имеющей дело с целочисленными топологическими размерностями (О - точка, 1 - линия, 2 - плоскость, 3 - объем). К фрактальным объектам отно­сятся все природные объекты, например, такие как береговая линия, имеющая размерность 1,52 (береговая линия Норвегии), облака - 2,31, кровеносная сис­тема человека - 2,7 и т.п. На данный момент обоснованной физической интер­претации дробной размерности нет, хотя предпринимаются попытки ее создать.

Основным свойством фракталов является самоподобие . В самом простом случае небольшая часть фрактала содержит информацию обо всем объекте, т.е. вид фракталов практически не меняется при любом увеличении. Определение фрактала, данное Мандельбротом, звучит так: «фракталом называется структу­ра, состоящая из частей, которые в каком-то смысле подобны целому». Процес­сы, порождающие самоподобные структуры , известны довольно давно. Это процессы с обратной связью , в которых одна и та же операция повторяется сно­ва и снова, при этом результат одной итерации является начальным значением следующей. Но здесь очень важно, чтобы зависимость между результатом и на­чальным значением была нелинейной. Одним из исследователей фракталов был Гастон Жюлиа, который открыл множество Жюлиа, представляющее собой границу, в различных частях которой встречается одна и та же форма разных масштабов. Он установил, что можно восстановить всю границу по любой ее части. С тех пор в математике и в физике стали широко изучаться самоподоб­ные структуры, в том числе и фракталы.

Все многообразие фракталов делится на геометрические, алгебраические и стохастические.

Геометрические фракталы самые наглядные. В случае, если геометриче­ские фракталы двухмерные их получают с помощью некоторой ломаной (или поверхности, если фракталы трехмерные), называемой затравкой или первона­чальным генератором. За один шаг алгоритма каждый из отрезков , составляю­щих ломаную, заменяется на ломаную-генератор в соответствующем масштабе. В результате бесконечного повторения этой процедуры получается геометриче­ский фрактал . На рисунках 1.1-1.6 представлены наиболее известные геомет­рические фракталы и их первоначальные генераторы.

Рис. 1.2. Кривая Коха (а) и ее первоначальный генератор (б)

Алгебраические фракталы . Это самая крупная группа фракталов. Получа­ют их с помощью нелинейных процессов в n-мерных пространствах. Наиболее изучены двухмерные процессы. Интерпретируя нелинейный итерационный процесс как дискретную динамическую систему, можно пользоваться термино­логией теории этих систем: фазовый портрет, установившийся процесс, ат­трактор и т.д. Известно, что нелинейные динамические системы обладают не­сколькими устойчивыми состояниями. То состояние, в котором оказалась ди­намическая система после некоторого числа итераций, зависит от ее начального состояния. Поэтому каждое устойчивое состояние (или, как говорят, аттрак­тор) обладает некоторой областью начальных состояний, из которых система обязательно попадет в рассматриваемые конечные состояния. Таким образом, фазовое пространство системы разбивается на области притяжения аттракто­ров. Если фазовым является двухмерное пространство, то, окрашивая области притяжения различными цветами, можно получить цветовой фазовый портрет системы (итерационного процесса). Меняя алгоритм выбора цвета, можно по­лучить сложные фрактальные картины с причудливыми многоцветными узора­ми. Неожиданностью для математиков стала возможность с помощью прими­тивных алгоритмов порождать очень сложные нетривиальные структуры. Ти­пичными представителями этого класса фракталов являются множества Жюлиа (рис. 1.7) и множество Мандельброта (Рис. 1.8).

Стохастические фракталы получаются в том случае, если в итерационном процессе случайным образом меняются какие-либо его параметры. При этом получаются объекты очень похожие на природные: несимметричные деревья, изрезанные береговые линии и т.д. Двумерные стохастические фракталы ис­пользуются при моделировании рельефа местности и поверхности моря.

Существуют и другие классификации фракталов, например, деление фрак­талов на детерминированные (алгебраические и геометрические) и недетерми­нированные (стохастические).

Контрольные вопросы

1. Кто и когда ввел понятия «фрактал» и «фрактальная геометрия»?

2. Что означает слово «фрактал»?

3. Почему фракталы нашли свое применение в человеческой деятельности?

4. Каково основное свойство фракталов?

5. На какие классы делятся фракталы?

6. Как образуются геометрические фракталы?

7. Что такое первоначальный генератор для геометрических фракталов?

8. Примеры геометрических фракталов.

9. Как образуются алгебраические фракталы?

10. Что такое аттрактор?

11. Примеры алгебраических фракталов.

12. Как образуются стохастические фракталы?

13. Примеры стохастических фракталов.

Чтобы понять, что такое фрактальная размерность, для примера рассмот­рим береговую линию Норвегии (рис. 1.9).

Какова ее длина? В масштабе карты хорошо видны глубокие фиорды на западном побережье. Идя вдоль берега, то и дело можно встретить скалы, острова, бухты и обрывы, которые похожи друг на друга, даже если они не обозначены на самых подробных картах. Прежде чем ответить на поставленный вопрос, необходимо решить, стоит ли включать в береговую линию острова. Как быть с реками? В каком месте фиорд переста­ет быть фиордом и где именно он переходит в реку? Ответить на эти вопросы иногда легко, иногда не очень. Но, даже если мы сумеем удовлетворительно от­ветить на все вопросы такого рода, одна трудность все же остается. Дело в том, что при измерении длины береговой линии, циркулю можно придать раствор, соответствующий км и сосчитать число шагов , которые понадобились бы, чтобы пройти по карте из конца в конец все побережье.

В спешке можно было бы выбрать раствор циркуля настолько большим, что не понадобилось бы заботиться даже о самых глубоких фиордах, и принять за длину береговой линии величину . Если подобная оценка не удов­летворяет, то можно выбрать несколько меньший раствор циркуля и повто­рить все сначала. На этот раз в длину береговой линии вошли бы и наиболее глубокие фиорды. Для еще более точного подсчета длины береговой линии по­надобятся более точные карты. Ясно, что при решении такого рода вопросов уточнения можно вносить бесконечно. Всякий раз, когда мы будем увеличивать разрешающую способность, длина береговой линии будет разрастаться. Кроме того, при использовании циркуля будут возникать проблемы с островами и ре­ками. Альтернативный способ измерения длины береговой линии состоит в том, чтобы покрыть карту сеткой, как показано в верхней части рисунка 1.9. Пусть квадратные ячейки сетки имеют размеры . Число таких ячеек, необходимых для покрытия береговой линии на карте, приблизительно равно числу шагов, за которое можно обойти по карте береговую линию циркулем с раствором . Уменьшение приводит к увеличению числа ячеек, необходимых для покрытия береговой линии. Если бы береговая линия Норвегии имела вполне определенную длину , то можно было бы ожидать, что число шагов циркуля или число квадратных ячеек , необходимых для покрытия берего­вой линии на карте, будет обратно пропорционально , а величина при уменьшении будет стремиться к постоянной . Однако это не так.

На рисунке 1.11 воспроизведен график (данные взяты из книги Мандельб­рота «Чему равна длина береговой линии Британии?»), на котором показана кажущаяся длина береговых линий и сухопутных границ. Все точки выстраи­ваются (в дважды логарифмическом масштабе) вдоль прямых. Угловой коэф­фициент этих прямых равен 1 - D где D - фрактальная размерность береговой линии (или сухопутной границы). Береговая линия Великобритании имеет D~ 1,3. Мандельброт приводит также данные для окружности и находит, что .

Контрольные вопросы:

1. Что такое размерность объекта?

2. Что такое топологическая размерность?

3. Как определяется фрактальная размерность природных объектов?

4. Чему равна фрактальная и топологическая размерности окружности,
груга, квадрата, сферы и шара?

5. Чему равна топологическая размерность береговой линии?